• Ratios And Unit Rates Pdf
• Rates Ratios And Unit Rates
• Unit 5 Percent Ratio And Ratewelcome
• Ratio And Unit Rate Quiz

Related Pages
Two-Term Ratio Word Problems
More Ratio Word Problems
Algebra Lessons

1. Specific Outcomes: 3) Demonstrate an understanding of percents greater than or equal to 0%. 4) Demonstrate an understanding of rate and ratio. 5) Solve problems that involve rates, ratios,.
2. Specific Outcomes: 3) Demonstrate an understanding of percents greater than or equal to 0%. 4) Demonstrate an understanding of rate and ratio. 5) Solve problems that involve rates, ratios, and proportional reasoning.
3. Ratios and Rates Khan Academy - Video - Ratios Introduction https://www.khanacademy.org/math/pre-algebra/pre-algebra-ratios-rates/pre-algebra-ratios-intro/v/ratios-intro.

Unit 5 – Percent, Ratio and Rate Grade 8 Mathematics L. Clemens P a g e 21 Percent Increase Percent increase is calculated when the price of an item goes up.Calculate the amount of increase by subtracting the original price from the new higher price. Example 1: The price of a can of soda increased from $0.95 to $1.25. Ratios, Rates and Unit Rates (2) STUDY. Terms in this set (14) unit rate. A rate that is simplified so that it has a denominator of 1. A comparison of two quantities by division. The greatest number that is a factor of two or more numbers.

Ratio problems are word problems that use ratios to relate the different items in the question.

The main things to be aware about for ratio problems are:

1. Change the quantities to the same unit if necessary.
2. Write the items in the ratio as a fraction.
3. Make sure that you have the same items in the numerator and denominator.

Ratio Problems: Two-Term Ratios

Example 1:
In a bag of red and green sweets, the ratio of red sweets to green sweets is 3:4. If the bag contains 120 green sweets, how many red sweets are there?

Solution:
Step 1: Assign variables:
Let x = number of red sweets.

Write the items in the ratio as a fraction.

Step 2: Solve the equation.
Cross Multiply
3 × 120 = 4 × x
360 = 4x

Isolate variable x

Answer: There are 90 red sweets.

Example 2:
John has 30 marbles, 18 of which are red and 12 of which are blue. Jane has 20 marbles, all of them either red or blue. If the ratio of the red marbles to the blue marbles is the same for both John and Jane, then John has how many more blue marbles than Jane?

Solution:
Step 1: Sentence: Jane has 20 marbles, all of them either red or blue.
Assign variables:
Let x = number of blue marbles for Jane
20 – x = number red marbles for Jane

We get the ratio from John
John has 30 marbles, 18 of which are red and 12 of which are blue.

We use the same ratio for Jane.

Step 2: Solve the equation

Cross Multiply
3 × x = 2 × (20 – x)
3x = 40 – 2x

Isolate variable x

John has 12 blue marbles. So, he has 12 – 8 = 4 more blue marbles than Jane.

Answer: John has 4 more blue marbles than Jane.

How To Solve Word Problems Using Proportions?

This is another word problem that involves ratio or proportion.

Example:
A recipe uses 5 cups of flour for every 2 cups of sugar. If I want to make a recipe using 8 cups of flour. How much sugar should I use?

• Show Video Lesson

How To Solve Proportion Word Problems?

When solving proportion word problems remember to have like units in the numerator and denominator of each ratio in the proportion.

Examples:

1. Biologist tagged 900 rabbits in Bryer Lake National Park. At a later date, they found 6 tagged rabbits in a sample of 2000. Estimate the total number of rabbits in Bryer Lake National Park.
2. Mel fills his gas tank up with 6 gallons of premium unleaded gas for a cost of $26.58. How much would it costs to fill an 18 gallon tank?3 If 4 US dollars can be exchanged for 1.75 Euros, how many Euros can be obtained for 144 US dollars?

Ratio problems: Three-term Ratios

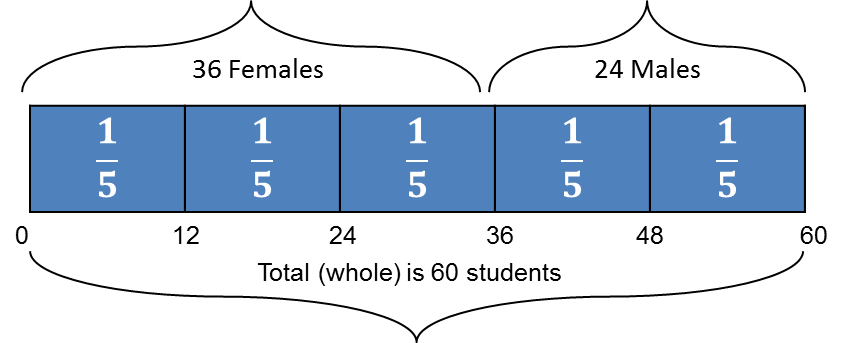
Example 1:
A special cereal mixture contains rice, wheat and corn in the ratio of 2:3:5. If a bag of the mixture contains 3 pounds of rice, how much corn does it contain?

Solution:
Step 1: Assign variables:
Let x = amount of corn

Write the items in the ratio as a fraction.

Step 2: Solve the equation
Cross Multiply
2 × x = 3 × 5
2x = 15

Isolate variable x

Answer: The mixture contains 7.5 pounds of corn.

Example 2:
Clothing store A sells T-shirts in only three colors: red, blue and green. The colors are in the ratio of 3 to 4 to 5. If the store has 20 blue T-shirts, how many T-shirts does it have altogether?

Solution:
Step 1: Assign variables:
Let x = number of red shirts
and y = number of green shirts

Ratios And Unit Rates Pdf

Write the items in the ratios as fractions.

Step 2: Solve the equation
Cross Multiply
3 × 20 = x × 4
60 = 4x
x = 15

5 × 20 = y × 4
100 = 4y
y = 25

The total number of shirts would be 15 + 25 + 20 = 60

Answer: There are 60 shirts.

Algebra And Ratios With Three Terms

Let’s study how algebra can help us think about ratios with more than two terms.

Example:
There are a total of 42 computers. Each computer runs one of three operating systems: OSX, Windows, Linux. The ratio of the computers running OSX, Windows, Linux is 2:5:7. Find the number of computers that are running each of the operating systems.

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

Rates Ratios And Unit Rates

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Unit 5 Percent Ratio And Ratewelcome

In chemistry and biology, the dilution ratio is the ratio of solute to solvent. It is often used for simple dilutions, one in which a unit volume of a liquid material of interest is combined with an appropriate volume of a solvent liquid to achieve the desired concentration. The diluted material must be thoroughly mixed to achieve the true dilution. For example, in a 1:5 dilution, with a 1:5 dilution ratio, entails combining 1 unit volume of solute (the material to be diluted) with 5 unit volumes of the solvent to give 6 total units of total volume.

This is often confused with 'dilution factor' which is an expression which describes the ratio of the aliquot volume to the final volume. Dilution factor is a notation often used in commercial assays. For example, in a 1:5 dilution, with a 1:5 dilution factor, (verbalize as '1 to 5' dilution) entails combining 1 unit volume of solute (the material to be diluted) with (approximately) 4 unit volumes of the solvent to give 5 units of total volume. Note that some solutions and mixtures take up slightly less volume than their components.

Ratio uses a colon ':', and 1:5 means 1+5 parts. Fraction '/' is the correct symbol which the previous author wishes to use, where 1/5 is 1 part is a total of 5.

The dilution factor can be expressed using exponents: 1:5 would be 5e−1 (5⁻¹ i.e. one-fifth:one); 1:100 would be 10e−2 (10⁻² i.e. one hundredth:one), and so on.

There is often confusion between dilution ratio (1:n meaning 1 part solute to n parts solvent) and dilution factor (1:n+1) where the second number (n+1) represents the total volume of solute + solvent. In scientific and serial dilution assays, the given dilution factor often means the ratio to the final volume, not to just the solvent. The factors then can easily be multiplied to give an overall dilution factor. Some have suggested that dilution factors should more clearly be written as a/total or a þ b, as the use of the colon symbol ':' is widely used to represent ratios in fields like mathematics, chemistry, or organic chemistry. Leave ratios for actual ratios 1:100 = 101. However, at this time, both dilution conventions are widely used -which is why it is important for laboratory personnel to always clarify whether a 'dilution ratio' or 'dilution factor' ought to be used in performing dilutions.

In analytical chemistry, dilution factor is always greater than 1 using equation,^[1]
${\displaystyle \text{dilution factor}=\frac{\text{final volume}}{\text{initial volume}}=\frac{\text{n+1}}{\text{1}}}$^[2]

or sometimes the inverse for other fields: ${\displaystyle \text{dilution factor}=\frac{\text{initial volume}}{\text{final volume}}=\frac{\text{1}}{\text{n+1}}}$^[3]

In other areas of science such as pharmacy, and in non-scientific usage, a dilution is normally given as a plain ratio of solvent to solute. For large factors, this confusion makes only a minor difference, but in precise work it can be important to make clear which ratio is intended.

In photographic development, dilutions are normally given in a '1+x' format. For example '1+49' would typically mean 1 part concentrate and 49 parts water, meaning a 500ml solution would require 10ml concentrate and 490ml water.

References[edit]

1. ^'Dilution Factor Chemistry'.
2. ^'Dilution factor calculation'.
3. ^'Mathbench serial dilution'.

See also[edit]

1. ^http://www.fclab.us/index.php/mediapress/10-in-the-press/13-dilution-confusion-conventions-for-defining-a-dilution

Ratio And Unit Rate Quiz